Backpropagation, dynamic programming and PyTorch

The other day I was vibing programming some coding problems and one thought strike me as odd. If dynamic programming is a memory optimziation of any recursion problems, wasn’t auto-diff on neuron network kinda of the same?

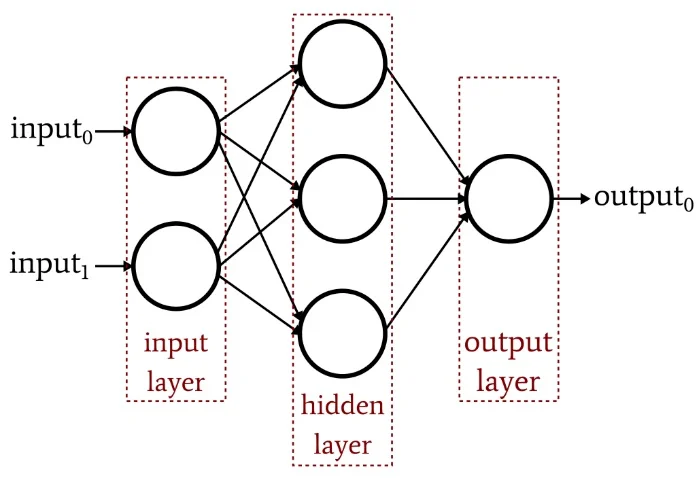
Start with a multilayer perceptron(MLP): each unit computes an activation on a dot product of a weight vector with its inputs. Training is first‑order optimization (gradient descent) on a loss; the work is to compute partial derivatives with respect to the weights.

Backpropagation is just the chain rule executed systematically on the computation graph. Slice the network into primitive functions, differentiate each, then compose derivatives along edges. One subtlety: although we picture the network as a function of inputs, the gradients we need are with respect to weights, so indexing must be kept straight.

Why it feels like dynamic programming: for any weight, you could expand the “downstream” derivative chain by hand, but many subchains repeat. Define δ at each node as the derivative of the loss with respect to that node’s pre‑activation (or chosen intermediate); these δ values are exactly the memoized subresults. Propagating δ from outputs back to inputs fills a table with the same shape as the network. Weight gradients then use local Jacobians times the stored δ, avoiding recomputation.

In short: chain rule + memoization (dynamic programming) = backpropagation. That’s the whole story, and it’s precisely what modern autodiff systems like PyTorch implement under the hood. And that also explains why we see this syntax sugar all the time in the modeling code:

import torch
### some training
loss = ...
loss.sum().loss()

Obviously both forward- and reverse-mode apply the chain rule, but reverse-mode (backpropagation) is preferred in neural network training for obvious reasons: forward-mode is efficient when inputs are few; reverse-mode is efficient when there are high-dimension inputs. Hence, in the snippet above:

loss.sum() ensures that you have a scalar value for backpropagation, especially when working with batches of data. use loss.mean() if you want the gradient update to be independent of the batch size
.backward() computes the gradients of the scalar loss w.r.t. all model parameters, which are then used to update the model during training via backpropagation.

Look deeper and we can see what PyTorch is really about. A python-leve tensor library api, which is largely modeled after NumPy, a auto-diff engine torch.autograd and a runtime library that can target different hardwares. And any modern large-scale machine learning system that aims to handle model training efficiently would more or less have the same functionalities, e.g. JAX. Of course, this is a over-simplication of PyTorch, which is arguably the backbone of modern-day machine learning. Throw some compilation between the first two you get torch.compile. And to make the runtime library works well with the tensor api you also need something like the PyTorch Dispatcher. There is a great blog from Edward Yang that you cannot miss.

And thats it for this post. Reach out if any questions or comments and stay tuned!